I recently saw an interesting proof for Pythagoras’s theorem in the MathHistory series which I wanted to share with y’all 🙂

So a quick reminder, Pythagoras’s theorem says that if we have a right-angle (90 degree) triangle, then there is the following relation between the length of the sides:

a = sqrt(b^2 + c^2) (where a is the length of the longest side) – and vice-versa.

The proof goes like this: lets rewrite the formula like a^2 = b^2 + c^2. We can interpret this geometrically as: (for a right-angled triangle) the are of the square constructed on the longer side is equal to the sum of the areas of the two squares constructed on the shorter sides.

And now the proof goes as follows:

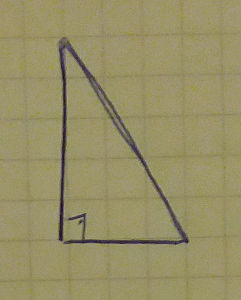
• consider a right angled triangle

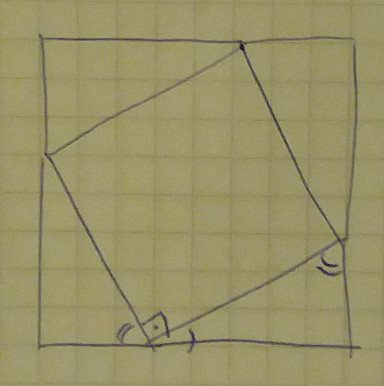
• "clone" it 4 times and put it together such that the longer sides form a square. Now the area of the inner square is a^2 while the area of the big square is a^2 + 4*At (At is the area of a triangle)

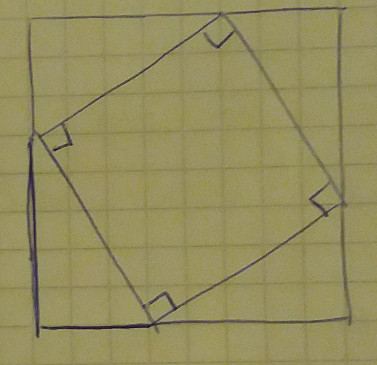
• rearrange the triangles as shown. The outer square is still of the same size (the length of its side – a+b is the same) but now it can be written as b^2 + c^2 + 4At. Hence a^2 + 4*At = b^2 + c^2 + 4At which can be simplified to a^2 = b^2 + c^2, or if you prefer to a = sqrt(b^2 + c^2).

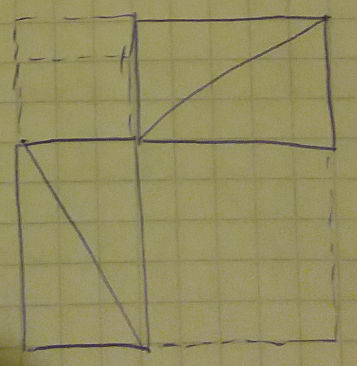
I only had one nagging feeling after seeing this proof – how do we know that the first big square constructed is actually a square. Can’t it be that its "edges" are not lines, but slightly crooked like below?

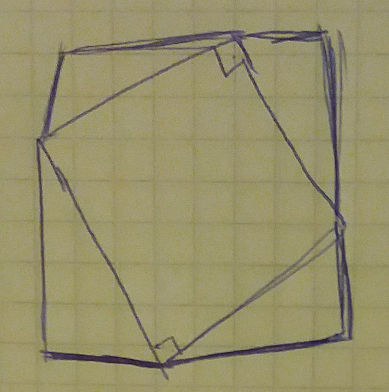
Fortunately we can use the fact that the angles in a triangle add up to 180 degrees (ie. a straight line) and show that the sides of the external triangle are indeed straight lines: